Fick’s Law plays a crucial role in elucidating the mechanisms behind gas diffusion, a fundamental process underpinning respiratory physiology and numerous engineering applications.
This expanded analysis aims to provide a thorough understanding of Fick’s Law, dissecting its components, implications, and practical relevance in a straightforward manner.
Key Takeaways:
- Fick’s Law quantifies the diffusion rate of gases across membranes, essential for understanding respiratory physiology.
- The diffusion rate is influenced by the membrane’s surface area, the gas’s partial pressure gradient, membrane thickness, and the diffusion coefficient.
- In medical contexts, Fick’s Law underpins the assessment of lung function and diagnoses of respiratory conditions.
- Beyond medicine, Fick’s Law is applied in environmental science, engineering, and biotechnology for pollution modeling, gas separation processes, and drug delivery systems.
- The concept of diffusing capacity integrates Fick’s Law’s variables, offering a practical measure of the lung’s efficiency in gas exchange.
Fundamental Principles
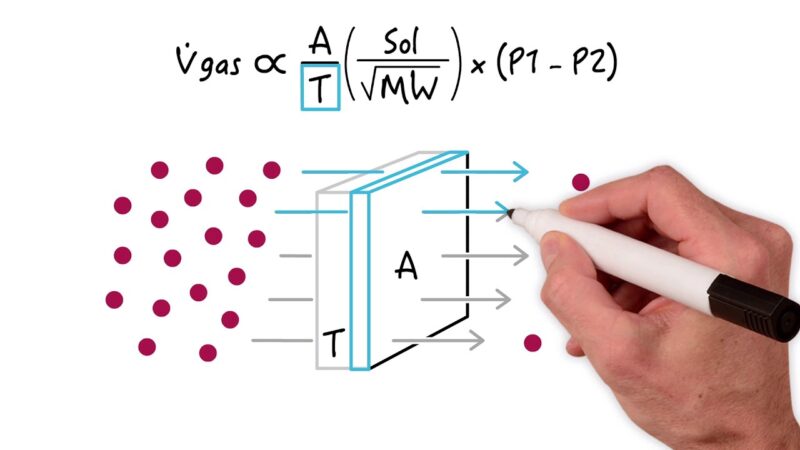
At its core, Fick’s Law describes how dissolved gases move across permeable membranes, driven by concentration gradients. This movement is quantifiable and predictable, governed by a set of variables encapsulated in the following equation:
- V’gas = D * A * ΔP/T
- V’gas = Rate of gas diffusion across permeable membrane
- D = Diffusion coefficient of that particular gas for that membrane
- A = Surface Area of the membrane
- ΔP = Difference in partial pressure of the gas across the membrane
- T = Thickness of the membrane
Dissecting the Equation
The equation highlights several key relationships:
- Diffusion Coefficient (�): This factor is determined by both the properties of the diffusing gas and the composition of the membrane. Gases with higher solubility in the membrane material and smaller molecular sizes tend to diffuse more readily.
- Surface Area (�): An increase in the membrane’s surface area enhances the rate of diffusion, providing more space for gas molecules to pass through.
- Partial Pressure Difference (Δ�): The driving force for diffusion is the concentration gradient, represented by the difference in partial pressure. Greater differences lead to higher diffusion rates.
- Membrane Thickness (�): Thicker membranes slow down the diffusion process by increasing the distance gases must travel to cross from one side to the other.
Application in Respiratory Physiology
Fick’s Law is essential for understanding gas exchange in the lungs, where oxygen must diffuse from the alveoli into the blood, and carbon dioxide must diffuse out. The law helps explain how variations in membrane thickness, surface area, or partial pressure gradients can affect respiratory efficiency. It also provides a framework for understanding how diseases that alter these variables can impair gas exchange.
The Concept of Diffusing Capacity
In physiological contexts, the diffusing capacity of the lung combines the variables of Fick’s Law into a single measure, reflecting the lung’s ability to facilitate gas exchange. This concept is particularly useful in clinical settings to assess and diagnose conditions that affect gas diffusion.
Relevance Beyond Medicine
Beyond its implications for respiratory physiology, Fick’s Law finds applications across various fields:
- Environmental Science: Understanding the diffusion of gases through air or water is crucial for modeling pollution dispersion and ecosystem dynamics.
- Engineering: In chemical and environmental engineering, Fick’s Law guides the design of systems for gas separation, ventilation, and controlled release of substances.
- Biotechnology: The principles of diffusion are applied in designing bioreactors and in drug delivery systems, where controlled diffusion of substances is critical.
FAQs
What is Fick’s Law?
Fick’s Law describes how the rate of gas diffusion across a membrane depends on the membrane’s characteristics, the gas’s partial pressure difference, and the diffusion coefficient.
How does Fick’s Law apply to respiratory physiology?
It explains the process of oxygen and carbon dioxide exchange in the lungs, highlighting how diseases affecting membrane thickness or surface area can impair gas exchange.
Can Fick’s Law be used outside of medicine?
Yes, it finds applications in environmental science for pollution dispersion, in engineering for designing ventilation systems, and in biotechnology for creating efficient drug delivery mechanisms.
What does diffusing capacity mean in the context of Fick’s Law?
Diffusing capacity is a measure derived from Fick’s Law to evaluate the lung’s effectiveness in transferring gas from the alveoli to the blood, integrating the law’s variables into a clinical assessment tool.
Conclusion
Fick’s Law offers a comprehensive framework for understanding and predicting the behavior of gases as they diffuse across membranes. By providing insight into the variables that influence diffusion, it serves as a vital tool in fields ranging from medicine to environmental engineering.
Its applicability in diagnosing respiratory diseases, designing medical devices, and solving environmental challenges underscores its importance across disciplines.
As such, Fick’s Law not only enhances our theoretical understanding of diffusion processes but also drives advancements in technology and healthcare